MATH 004: Intermediate Algebra

Sets and Operations with Real Numbers

---

Reading Assignment:

Nustad and Wesner: Sections 1-1 and 1-2, pages 2-10 and pages 13-20.

 

Learning Objectives

After completing this lesson, you will be able to:

• understand terminology associated with sets
• determine when a given set is a subset of another set
• perform the operations of union and intersection on sets
• use inequalities to determine relationships between given numbers
• find the absolute value of a number
• perform the basic arithmetic operations on all real numbers
• understand and simplify exponential expressions
• perform the basic arithmetic operations on fractions

 

To continue to the next page, click on next at the top or bottom of the page (on the right side.)

Lesson 1 Commentary

At the beginning of the study of a subject, it is customary to review all the language and basic definitions used by that subject. This is also true in the study of algebra, and the first three lessons of this course will be spent reviewing this necessary background material.

During the first lesson we will be covering the following topics:

• Set Notation
• Union of Sets
• Number Systems
• The Real Number Line
• Absolute Value
• Operations with Real Numbers
• Multiplication/Division
• Division by Zero
• Fractions- Addition/Multiplication/Division
• Exponential Expression

To continue to the next page, click on next at the top or bottom of the page (on the right side.)

To continue to the next page, click on next at the top or bottom of the page (on the right side.)

Union of Sets

Operations can be performed on two sets to create a new set. These operations are called union and intersection of sets. When the union of two sets is formed, a new set is formed that contains all the elements found in the first set, all the elements in the second set, and all the elements in common between the two sets. In short, if an element is found in either of the sets, it is found in the union—everything is in the union of two sets. The union of sets is denoted by the symbol $\cup$ .

Examples

By using the sets A, B, C and D from the previous page:

1. $A\cup B=\left\{1,2,3,4\right\}\cup \left\{4,5,6,7\right\}=\left\{1,2,3,4,5,6,7\right\}$

Remember- elements are listed only once in a set.

2. $C\cup D=\left\{4,5\right\}\cup \left\{9\right\}=\left\{4,5,9\right\}$

 

To continue to the next page, click on next at the top or bottom of the page (on the right side.)

Intersection of Sets

When two sets are intersected, a new set is formed containing the elements found in both the first set and the second set. In other words, the elements that are shared by both sets are found in the intersection.

The intersection of sets is denoted by $\cap$.

Examples

By using the sets A, B, C and D from the previous page:

$A\cap B=\left\{1,2,3,4\right\}\cap \left\{4,5,6,7\right\}=\left\{4\right\}$

$B\cap C=\left\{4,5,6,7\right\}\cap \left\{4,5\right\}=\left\{4,5\right\}=C$

$C\cap D=\left\{4,5\right\}\cap \left\{9\right\}=$$\varnothing$

$\left(A\cup B\right)\cap C=\left(\left\{1,2,3,4\right\}\cup \left\{4,5,6,7\right\}\right)\cap C$

$=\left\{1,2,3,4,5,6,7\right\}\cap \left\{4,5\right\}$

$=\left\{4,5\right\}$

$=C$

 

Note: In the second example, the result of the intersection happens to be one of the defined sets. In the third example, we got the empty set $\varnothing$ and so the sets are said to be disjoint.

 

To continue to the next page, click on next at the top or bottom of the page (on the right side.)

Number Systems

Set notation can be used to define each of the number systems. All numbers are built up from the natural numbers. Since these numbers can be counted on one’s fingers, they are also called the counting numbers.

 

The natural numbers are defined as: N= {1,2,3...}

 

The use of the ... shows that the natural numbers are never ending, or an infinite set.

By adding the element 0 to the natural numbers, the whole numbers defined as: W= {0,1,2,3,...}.

Adding a sequence of negative natural numbers to the set W defines the integers, defined as:

J= {..., -2,-1,0,1,2...}.

 

To define the next number system, a new type of set notation is needed. Set-builder notation provides the rules and constraints for constructing, or building, each element of the set. The rational numbers do not follow a sequence as the previous number systems did.

Using set-builder notation, the rational numbers are defined as:

In words, this is read "the set of all p over q such that p and q are integers with q not equal to zero."

The rational numbers can also be described as all numbers whose decimal representation is either terminating

(like $\frac{1}{2}=.5$ ) or repeating (like $\frac{1}{3}=.333$... )

 

The irrational numbers are the next number system, and they do not contain any elements of the previously defined sets of numbers.

The irrational numbers are defined as those numbers whose decimal representation is both non-terminating and non-repeating. This set is represented by the letter H. Examples of irrational numbers are $\pi$ and $\sqrt{2}$ .

The final number system covered in this course is the real numbers, represented by the letter R.

The real numbers are defined as the union of the set of all rational numbers with the set of all irrational numbers.

That is, R= Q ∪ H. Unless otherwise specified, the work in this course will involve the real numbers.

The real numbers can be pictured as follows:

Reals
Rationals			Irrationals
..., $\frac{1}{2}$, $\frac{3}{4}$ , $\frac{-7}{6}$ , ... Integers Negative   Positive ..., -2, -1, 0, 1, 2, ...			..., $\sqrt{2}$, $\sqrt[3]{5}$, $\pi$, ...

 

To continue to the next page, click on next at the top or bottom of the page (on the right side.)

Real Number Line and Absolute Value

The real numbers can be represented on a number line. This number line can be helpful in determining whether or not one number is greater than another. One number that is to the right of another on the real line is the greater of the two.

Since 4 is to the right of −2, 4 is greater than −2. Symbolically, this is expressed as 4 > −2.

This type of inequality symbol is known as a strict inequality. Notice that the arrow points to the lesser number.

In later lessons, a weak inequality symbol will be used. This is an inequality sign with a line underneath: ≥ or ≤.

The line underneath allows for the possibility of both sides being equal.

 

Absolute Value

The method used to measure the distance of a number from zero (regardless of which side of zero the number appears on) is known as absolute value.

Since absolute value measures a distance, it is never equal to a negative number. Absolute value is denoted by placing the number inside | |, such as |3| or | − 5|.

 

Examples

| − 4| = 4 (since −4 sits 4 units from 0)

|6| = 6 (since 6 sits 6 units from 0)

Occasionally, there is another sign placed outside the absolute value sign, such as in −| − 7|.

This is actually indicating that two operations are taking place.

−| − 7| first, find the absolute value of − 7 : | − 7| = 7

second, find the opposite of 7 : −7

so, − | − 7| = −7

 

The formal definition of absolute value is the following: for a real number x, the absolute value of x is defined as follows:

 

To continue to the next page, click on next at the top or bottom of the page (on the right side.)

Operation with Real Numbers

The rules for the basic arithmetic operations, addition, subtraction, multiplication and division on signed numbers will be discussed in this section. No calculators should be used when practicing these operations—these are skills also required for future operations on the terms of algebraic expressions.

Addition/Subtraction

The real number line can be used to visualize the addition and subtraction of signed numbers, until one becomes comfortable with the operations. The following rules can be used:

— adding a positive number → move right
— subtracting a positive number → move left
— adding a negative number → move left (notice this is the same action as subtracting a positive number)
— subtracting a negative number → move right (notice this is the same action as adding a positive number)

Examples

1. $3+(-7)$ — in this case, a negative is being added. Use 3 as the starting point, then move 7 spaces to the left.

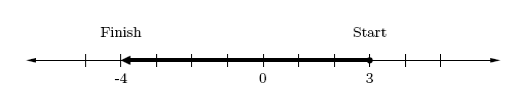
So,   $3+\left(-7\right)=-4$ .

 

2. $\left(-2\right)+\mathrm{3 }$ — in this case, a positive is being added. Use -2 as the starting point, then move 3 spaces to the right.

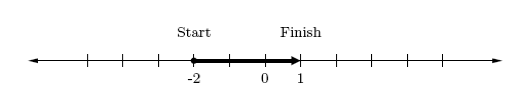
So,   $\left(-2\right)+3=1$ .

 

 

3. $2-(-6)$ — in this case, a negative is being subtracted. Use 2 as the starting point, then move 6 spaces to the right.

 

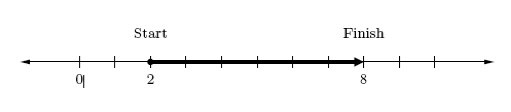
So,   $2-\left(-6\right)=8$ .

 

 

4. $-2-7=-2-(7)$ — in this case, a positive is being subtracted. Use -2 as the starting point, then move 7 spaces to the left.

 

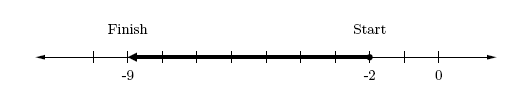
So,   $-2-7=-2-\left(7\right)=-9$ .

 

To continue to the next page, click on next at the top or bottom of the page (on the right side.)

Multiplication/Division

In a multiplication problem, those numbers (or later, variables) that are being multiplied are called factors; the result of a multiplication problem is called a product.

In algebra, multiplication is not indicated using the × sign (since × is often the variable of choice!). Instead, multiplication can be expressed using a dot, as in 2·3 = 6 (here, 2 and 3 are the factors and 6 is the product), or by using parentheses as in

(−7)(3) = −21.

In arithmetic, division is usually written as either 36 ÷ 4 = 9, or 

$4\begin{array}{c}\hfill 9\\ \hfill \overline{)36}\end{array}$

Using this example, 36 is known as the dividend, 4 is the divisor, and the result 9 is called the quotient.

In algebra, however, division is typically expressed in a fractional form.

The rules for multiplying and dividing signed numbers involve counting the number of negative signs in the problem. These rules apply to problems involving multiplication only, division only, or multiplication and division combined.

Use these rules to determine the sign of a product or quotient:  $\frac{36}{4}=9$ or $36/4=9$ .

— If there are an even number of negative signs, the product/quotient is positive.

— If there are an odd number of negative signs, the product/quotient is negative.

PLEASE NOTE:

The following links as well as all of the examples throughout this course will open in a new window.

Please close the window to return to the lesson.

Example 1_7

$\left(-5\right)\left(-6\right)\left(-2\right)$

Example 1_7_2

$\frac{\left(-3\right)\left(-2\right)\left(4\right)}{\left(-2\right)\left(-2\right)}$

 

To continue to the next page, click on next at the top or bottom of the page (on the right side.)

Division by Zero

Division by zero is undefined. This word, undefined, is the stated result of any division problem with a zero divisor.

Click on the link below to see example 1_8 in a new window. When you are finished close the window to return to the lesson.

Example 1_8

$\frac{8}{0}$ and $\frac{\left(7\right)\left(-2\right)\left(3\right)}{\left(4\right)\left(0\right)\left(-6\right)}$

 

To continue to the next page, click on next at the top or bottom of the page (on the right side.)

Fractions

Knowledge of the basic arithmetic operations on fractions is very important to both everyday life and future algebra courses.

In those courses, students are expected to add, subtract, multiply and divide rational expressions, which are algebraic expressions that are fractional in form.

Recall that each fraction is made up of a numerator (the top part) and a denominator (the bottom part).

 

Addition/Subtraction of Fractions

Express each fraction in terms of a common denominator; then, add or subtract the numerators as dictated in the problem.

Don’t forget to reduce to lowest terms when finished.

Click on the link below to see example 1_8_2 in a new window. When you are finished close the window to return to the lesson.

Example 1_8_2

$\frac{1}{2}+\frac{1}{3}$ and $\frac{5}{6}-\frac{1}{3}$

 

Multiplication of Fractions

Multiply numerator with numerator, and denominator with denominator. Finish by reducing to lowest terms.

Click on the link below to see example 1_8_3 in a new window. When you are finished close the window to return to the lesson.

Example 1_8_3

$\frac{2}{3}·\frac{3}{4}$

 

Division of Fractions

To divide fractions, find the reciprocal of the divisor (that is, invert numerator and denominator) and change from a division sign to multiplication. If necessary, reduce to lowest terms.

Click on the link below to see example 1_9 in a new window. When you are finished close the window to return to the lesson.

Example 1_9

$\frac{3}{4}÷\frac{7}{2}$ and $\frac{7}{9}÷\frac{2}{3}$

 

To continue to the next page, click on next at the top or bottom of the page (on the right side.)

Exponential Expressions

Repeated multiplication of one factor can be expressed in a shorthand notation known as an exponential expression.

For example, 3 · 3 · 3 · 3 can be written as $3^4$.

The repeated factor, in this case the 3, is called the base. The number of times the 3 appears as a factor in the product, in this expression the 4, is known as the exponent.

An exponential expression written in its long form, 3 · 3 · 3 · 3, is called the expanded form.

The work in this section will be confined to numeric bases; in later lessons, exponential expressions with variable bases will be developed. Exponential expressions that have numbers as bases can be simplified—that is, the multiplication can be carried out and a product determined.

• If a base is a positive number, then the product represented by the exponential expression will always be positive.
• If the base is negative, then the exponent determines whether the product is positive or negative.

Recognizing a negative base in an exponential expression can be tricky. The simplest way to distinguish a negative base is to remember that such a base is always contained in parentheses.

Examples of negative bases are:

${\left(-3\right)}^5$ or ${\left(-1\right)}^6$

An exponent only acts upon the base that immediately precedes it. Placing the negative number inside parentheses is the way of showing that an exponent is acting upon a negative base. So in expanded form,

${\left(-3\right)}^5=\left(-3\right)\left(-3\right)\left(-3\right)\left(-3\right)\left(-3\right)$ and

${\left(-1\right)}^6=\left(-1\right)\left(-1\right)\left(-1\right)\left(-1\right)\left(-1\right)\left(-1\right)$

Contrast these with an exponential expression such as the following: −72. Since the base is not contained in parentheses, this expression does not have a negative base. Instead, there are actually two operations occurring—first, the exponent of 2 acts upon the 7, then second, the opposite of the quantity is found. Thus,

$-7^2=-\left(7^2\right)=-\left(7·7\right)=-\left(49\right)=-49$

The rules for simplifying exponential expressions with negative bases are an extension of the rules for multiplying and dividing signed numbers. If a negative base is raised to an even exponent, the resulting product will be positive. If a negative base is raised to an odd exponent, the resulting product will be negative.

Click on the link below to see example 1_10 in a new window. When you are finished close the window to return to the lesson.

Example 1_10

${\left(-3\right)}^5$ and ${\left(-2\right)}^4$

 

To continue to the next page, click on next at the top or bottom of the page (on the right side.)

Practice Problems Set 1

Please complete the practice problems below with a paper and pencil. You may check your work at the end of the set by clicking on "SOLUTIONS."

Given sets A={5,6,7}, B={1,2,3,4,6}, C={8,9,10} and D={1,7,9} form the following sets:

1. $A\cup B=$

2. $A\cap C=$

3. $\left(A\cup C\right)\cap B=$

4. $B\cap D=$

5. $\left(A\cap B\right)\cup \left(C\cap D\right)=$

Solutions. This link will open in a new window.

 

To continue to the next page, click on next at the top or bottom of the page (on the right side.)

Practice Problems Set 2

Please complete the practice problems below with a paper and pencil. You may check your work at the end of the set by clicking on "SOLUTIONS."

Use >, < or = to indicate the relationship in each of the following:

6. $-5$ ______ $-10$

7. $\left|-5\right|$ ______ $\left|-10\right|$

8. $\; \left|-5\right|$ ______ $\left|5\right|$

9. $-\left|-5\right|$ ______ $\left|5\right|$

 

Solutions. This link will open in a new window.

 

To continue to the next page, click on next at the top or bottom of the page (on the right side.)

Practice Problems Set 3

Please complete the practice problems below with a paper and pencil. You may check your work at the end of the set by clicking on "SOLUTIONS."

Perform the indicated operations:

10. $\left(-8\right)-\left(7\right)+\left(3\right)-\left(2\right)=$

11. $\left(-2\right)\left(6\right)\left(-3\right)=$

12. ${\left(-3\right)}^4=$

13. $-3^4=$

14. $\frac{\left(-18\right)\left(12\right)}{\left(-9\right)\left(6\right)}=$

 

Solutions. This link will open in a new window.

 

To continue to the next page, click on next at the top or bottom of the page (on the right side.)

Practice Problems Set 4

Please complete the practice problems below with a paper and pencil. You may check your work at the end of the set by clicking on "SOLUTIONS."

15. $\frac{\left(-14\right)\left(12\right)}{\left(-4\right)\left(-7\right)}=$

16. $\frac{5}{12}-\frac{1}{8}=$

17. $\frac{5}{9}+\frac{2}{3}=$

18. $\frac{7}{16}÷\frac{1}{20}=$

19. $\frac{3}{8}÷9=$

20. $\frac{3}{8}·\frac{7}{12}=$

 

Solutions. This link will open in a new window.

 

To continue to the next page, click on next at the top or bottom of the page (on the right side.)

Lesson 1 Wrap Up

You have now reached the end of lesson 1.

For a review of the terms presented in this lesson please complete the Lesson 1 Terms Check.

Please complete these problems with your Wacom Bamboo USB Tablet with Cordless Pen. Then submit your work to the Lesson 1 homework drop box.

Exercise 1–1, pages 10–13, problems: 13, 15, 19, 21, 25, 29, 31, 39, 45, 49, 61, 63, 65, 69.

Exercise 1−2, pages 20−23, problems: 15, 17, 21, 31, 35, 41, 45, 65, 75, 88.

Take Quiz 1

For instructions on the Wacom Bamboo USB Tablet with Cordless Pen please see the homework submission help.

You may also access the activities by clicking on the Activities link in the left hand side menu and the click into the Lesson Materials folder.

 

To continue to the next page, click on next at the top or bottom of the page (on the right side.)