MATH 017: Finite Mathematics

Lesson 1: Set Theory: Relations and Operations

Properties of Sets

De Morgan's Properties

Two more properties dealing with set operations and complements are known as De Morgan's properties.

$\overline{A\cup B}=\bar{A}\cap \bar{B}$ , and

$\overline{A\cap B}=\bar{A}\cup \bar{B}$

How would you go about proving these properties are true? You could pick some set to be the universal set. Next, define A and B and their complements. Then show that the properties are true. But this would only show that the property holds for this specific example; we need to show that it works all the time.

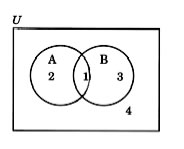
To show it works for all sets we could use a Venn diagram that demonstrates all the possibilities when considering any two sets in a general universal set. Note the following Venn diagram and how its particular configuration covers all possible cases with two sets in a particular universal set.

The numbers in the following Venn diagram will be used to denote certain areas in the upcoming discussion.

Figure 1.2 Venn Diagram Text Alternative

Venn diagram shows 2 intersecting circles, one labeled A, one labeled B, within a rectangular shape labeled U surrounding them. Cirlce A has a 2 in it that is outside of circle B; Circle B has a 3 in it that is outside of circle A and the intersection of the two circles has a 1 in it. The area outside the circles but inside of the rectangle has a 4 in it.

Area #1 denotes the intersection of sets A and B.

Areas #1 and #2 denote set A.

Areas #1 and #3 denote set B.

Area #4 denotes the area in the universal set not in A or B.

$A\cup B$ would be areas [#1, #2, and #3].

$A\cap B$ would be area [#1].

$\bar{A}$ complement is areas [#3 and #4].

$\bar{B}$ complement is areas [#2 and #4].

Now let's prove the first of De Morgan's properties: $\overline{A\cup B}=\bar{A}\cap \bar{B}$ .

To determine the left side of the equation we realize that A∪B is area [#1, #2, and #3], so the complement of those areas would be area #4. Therefore the left side gives area #4.

To determine the right side of the equation understand that A is area [#1 and #2], so the complement of A is area [#3 and #4].

B is area [#1 and #3], so the complement of B is area [#2 and #4].

The intersection of A complement and B complement is area #4. Therefore, left and right sides of the equation match and the first property is proven.

Can you prove De Morgan's second property?  Why don't you try it and when you think that you have it figured out, click to see the Instructor's Solution.

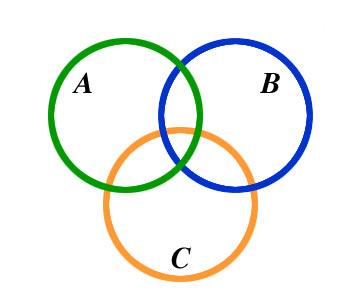
Note the Venn diagram, below. In this Venn diagram we have three sets in our universal set and a total of eight areas we could use as areas to reference. Every time that a new set is added the number of different areas doubles.

Figure 1.1 Venn Diagram Text Alternative

Example of Venn diagram shows 3 intersecting circles labeled A, B and C. The circles intersect in such a way that each pair of circles intersects and all three circles intersect in a center area. The three are surrounded by a rectangle that represents the universal set.