Exercise 7.2: Problem 14 Transcript | Exercise 7.2: Problem 32 Transcript | Exercise 7.2: Problem 38 Transcript

Exercise 7.2: Problem 14 Transcript

We're going to look at problem number 14 in section 7.2 here. We're working with the number of elements in a set. We're going to do this one a couple of different ways using a Venn diagram, and also using the formulas. So, number 14.

The information that we're given is that the number of elements in A is 10. The number of elements in A intersect B is 5. And the number of elements in A union B is 29. And we're supposed to find the number of elements in B.

$\begin{array}{l}n\left(A\right)=10\hfill \\ n\left(A{{\displaystyle \cap }}^{\text{}}B\right)=5\hfill \\ n\left(A{{\displaystyle \cup }}^{\text{}}B\right)=29\hfill \\ \text{Find }n\left(B\right)=\text{?}\hfill \end{array}$

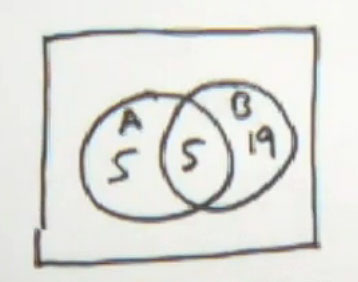
So let's do that using a Venn diagram first. And then we'll go through it using the formulas. I lean towards Venn diagrams a little bit. Students generally have more success once they learn how to do these. But in a lot of cases, the formulas work perfectly well, also. So there's your two set Venn diagram. We only have two sets here.

You always need to fill in the area that is given to you with two pieces of information. You can't put the number 10 anywhere on here, because the number of elements in A is 10. That includes this area and this area. Some of the 10 are going to be in here, and some are going to be in here.

However, we do know that the number of elements in A intersect B is 5, so we do this. Now of course, if the total inside the a circle has to be 10, and this is 5, then this is going to be 10 minus 5, and this one is also going to be 5. Now we have 10 inside the a circle, 5 inside A intersect B.

Now, we also this piece of information that the number of elements in A union B is 29. So the total inside the two circles has to be 29. There's 10 here. That means 29 minus 10 is 19 have to be inside that B circle. So how many are inside B? Well, not 19. But inside that B circle, the total inside the B circle is 24. Sorry. 19 plus 5.

Now, we can also do that using a formula. Remember the formula n of A union B is equal to n of A plus n of B minus n of A intersect B.

$n\left(A\cup B\right)=n\left(A\right)+n\left(B\right)-n\left(A\cap B\right)$

The formulas work perfectly well in a lot of cases, not in all cases. We know this is 29. We know that this is 10. We know that we're looking for this one. And we know that this is 5.

$29=10+n\left(B\right)-5$

So this is 29 equals 5 plus n of B. And bring the 5 over, solving this algebraically. And then n of B is equal to 24. So you could do it that way, also. In this case it's probably a little easier to use the formula, but there's a lot of cases where the Venn diagram is the way to go. So there's two different ways to do the same problem. OK.

$\underset{-5}{29}=\underset{-5}{5}+n\left(B\right)$
$n\left(B\right)=24$

Exercise 7.2: Problem 32 Transcript

We're going to look at question 32 from section 7.2. This is a table. I'm not going to recopy the table for you, that's in your textbook. It's a table, a contingency table that looks at the industry type for CEOs as well as the region that they're in. Industry types are manufacturing, communications, or finance. And then the regions are Northeast, Southeast, and Midwest. And all we're going to do is do some totals here.

Part a, the question is, What is the number of CEOs whose response was not Southeast? So not Southeast, of course, is Northeast, or Midwest, or West. Or means add.

There are 102 in the Northeast. That's 37 + 35 + 30. In the Midwest there are 52. 27 + 15 + 10, which is 52. In the West, there are 53. 15 + 20 is 35 + 18 is 53. And that gives us a total of 207.

NE=102
MW=52
W=53
102+52+53=207

Part b. So on the other hand, in part b they ask us for the number of CEOs whose responsible was communications or West. Now there in the West, we already decided there were 53. In the communications, 35 + 23 + 15 + 20 is 93. So, communications. There are 93. In the West there are 53.

And communications or West, you might think of them as just being 93 + 53. But you have to be a little bit careful here. Seems like you might have double counted something. Those people that are in communications and in the West are actually counted in the West column, and they're also counted in the communications row. You don't want to double count that.

So we should subtract that 20 off once, and that will bring it back to the count that we want. So comm or West is going to be 93 + 53 - 20 and that is 126. Add them together, subtract off the one that you counted twice, and now you're only counting it once.

Comm=93
West=53
Comm or West= 93+53-20=126

In Part c, we want the number of CEOs whose response was Northeast, but not manufacturing. So Northeast, but not manufacturing is just our 35 plus our 30 for communications and finance. And that is a total of 65.

35+30=65

Part d. On the other hand, in part d, the number of CEOs whose response was manufacturing or communications or Midwest or West, let's see, that's manufacturing the first two rows. Total those up. Or Midwest. And West. So the last two columns, we could total those up. Add those all together, make sure we didn't double count too much stuff. Subtract it off if we did, but there's actually going to be an easier way to do this. That seems complicated.

If we take manufacturing communications, West and Midwest, that fills out the entire top right part of that table, and only leaves the finance Northeast, and finance Southeast blank. So instead of counting everything that we want to include in, we just throw away the things we don't want using the complement. That's going to be an easier way to do that.

So we know there are a total of 250 CEOs, and we're going to subtract off the 30 and the 12 that came from Northeast and Southeast in finance.

That's 250 - 42, which is 208. So that's a far easier way to do that than adding all those other numbers.

250-(30+12)=208

OK.

Exercise 7.2: Problem 38 Transcript

We're going to look at problem number 38 from section 7.2. This is a problem that's most easily done using a Venn diagram. This is a three-set problem. It's a survey of 75 business travelers, and it's a survey of what they normally read - which newspaper. So I'm not to read off all the numbers to you, I'll leave that to you.

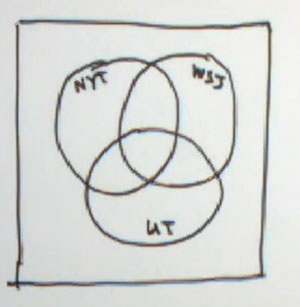
But we have The New York Times, The Wall Street Journal, and USA Today that we're going to be working with as our newspapers. You need to fill these in very carefully. This will be The New York Times. This will be The Wall Street Journal. And this will be USA Today. So they give us numbers. How many read The New York Times, how many read the Wall Street Journal, etc., and then they give us combinations.

New York Times and Wall Street Journal, New York Times and USA Today. And they give us all three. We just have to start in the middle, with all three. So they tell us that there are 5 that read all three. And then we have to work out slowly. This has to be done just right. They tell us that 8 read The Wall Street Journal and USA Today.

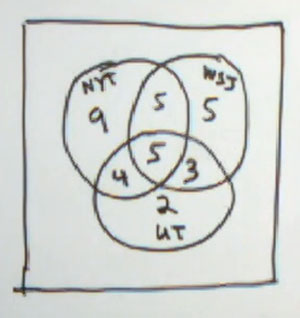
So you know that in here, between The Wall Street Journal and USA Today is going to be 8. Now, 5 of them are here, so you need to make sure you subtract at this point to get the 3 there. That's a total of 8 that read The Wall Street Journal and USA Today. On the other hand, they tell us that nine read the New York Times and USA Today.

Five are here. At least 4 for right there. Make sure you're subtracting as you're filling these in. 10 read The New York Times and The Wall Street Journal. 5 here, 5 here. We're going to have to subtract again in this next set of steps. They tell us that 14 read USA Today. There's a total of 12 right here that are inside the USA Today circle.

So we only need two more to get the total up to 14 that read USA Today. On the other hand, they tell us that 18 read The Wall Street Journal. There's 13 already inside The Wall Street Journal circle. So we need 5 more to make that total 18. 23 read The New York Times. There are 14 right there.

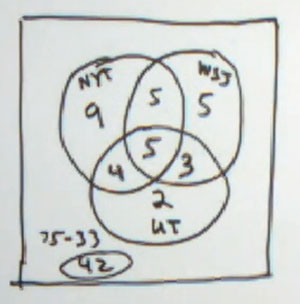
That leaves 9 for inside The New York Times circle, but outside the other circles. Now, there are a total of 75 business travelers. Let's see, there's 23 right here. There's 31 right there. There's 33 right there. And that means outside we have 75 minus 33, which is 42 that are inside any of those circles. OK.

So we've got our Venn diagram all filled in now, we're ready to start answering questions.

Part a. how many read none of these three magazines? That's the 42 we just found.

Part b. How many read The New York Times alone. That means The New York Times and neither of the other two. That's our nine. right there.

Part c. How many read The Wall Street Journal alone? That is our 5 right there. Wall Street Journal but none of the other - 2.

Part d. And USA Today only. And that is this 2 right here.

Part e. How many read neither The New York Times nor The Wall Street Journal. So they don't read The New York Times, and they don't read The Wall Street Journal.

So you can't include anything that's inside either of those two circles. And if you're not thinking very carefully, you might think that that's just 2. But we also have this 42 down here, and they certainly don't read The New York Times or Wall Street Journal. So we have 2 plus 42, which is 44.

And Part f. How many read The New York Times or Wall Street Journal, or both? So all of The New York Times people, all the Wall Street Journal people. And all those that are both, of course. Well, there were 23 inside The New York Times circle plus 5 plus 3 23 Plus 5 plus 3 is 31.

So that's how you want to do that, filling that Venn diagram in carefully. Making sure you subtract at each step, and then picking out the important areas, and sometimes it might be more than one. OK.