MATH 017: Finite Mathematics
Lesson 1: Set Theory: Relations and Operations
Lesson 1 Introduction
In this first lesson for Finite Mathematics we introduce the basic concepts and tools used in set theory. The lesson begins with a discussion of what a set is, how it can be identified and explains the difference between finite and infinite sets. From there it moves to a discussion of the ways that two sets relate; this includes equality and other relationships. Some operations on sets are described next with a focus on “union” and “intersection”. And finally the discussion turns to a pictorial representation of sets in Venn diagrams. Welcome and enjoy, as I do, the wonder of sets.
For each lesson, read the Learning Objectives and Textbook Reading Assignment first and then read the Lesson notes in Canvas. Be sure to work through the Example problems as you read your textbook assignment. You should do the same with the examples in your online Lesson notes.
Learning Objectives
- Utilize both the roster and set-builder notation to describe a set of elements
- Compare and contrast finite and infinite sets
- Define the empty set and designate it with the proper notation
- Recognize the equality of two sets
- Recognize when one set is a subset of another set
- Define the union and intersection of sets
- Describe the properties of set union and intersection
- Identify the difference between two sets
- Define the term disjoint set
- Create Venn diagrams and use them properly
Lesson Readings & Activities
By the end of this lesson, make sure you have completed the readings and activities found in the Lesson 1 Course Schedule.
Sets
A set is a well-defined collection of objects.
By well-defined we mean that you are able to answer the following question: "Is a particular element in the set?" For example, let's consider the collection of names of United States presidents. We can definitely answer the question, "Is Abraham Lincoln in this collection of names of U.S. presidents?" On the other hand, suppose you have a collection of large animals. Would a horse be in this collection? Most people would say yes to that question, but suppose you asked about a collie dog? You begin to understand the meaning of well-defined here when someone asks how large is large. Large, small, good, bad, young, old -- these are all terms that are not automatically well defined and could easily cause a collection of objects not to be classified as a set.
Describing a Set
A set can be described two ways—by roster method or by using set-builder notation.
Roster Method
The roster method simply lists all the elements in the set. For example, set A could be described using braces like this:
A = {1, 2, 3, 4, 5}.
We could easily tell what is in the set by just looking at it. The above is a finite set, meaning you can count the number of objects in the set.
Another version of the roster method that is used when dealing with infinite set is sometimes called the modified roster method because it uses an ellipsis, " … ", to show that it follows a given pattern to infinity. For example, B = {1, 2, 3, } would be the infinite set of all positive integers.
The modified roster method can also be used on finite sets where there are many terms that follow a pattern. For example, C = {1, 2, 3, 100} would be the set of positive integers from one to one hundred. Here, the three dots show that the numbers follow the pattern set up by the first three numbers to one hundred.
Note: In set B above, we cannot list all the numbers and we cannot count them, so set B is an infinite set.
If a set is described using the roster method, you must use braces to enclose the elements.
Set-Builder Notation
The second method of describing a set is set-builder notation, where a set is described using the following format:
A = {x | x is an even integer > 0}
It would be read as "A is the set of all x such that x is an even integer greater than zero." This set would look like the following using the roster method:
A = {2, 4, 6, }.
The set-builder notation method can also be used to describe a set that would be cumbersome using the roster method. For example,
A = { x | x is a city in the U.S. that has more than 5,000 people living in it}.
You can imagine how many cities would be in this set!
Empty Set
Now that we know what a set is and can describe it, we need to talk about a very special set called the empty set or the null set. The more common name is empty set. It is defined as the set having no elements and is denoted by the symbol or by empty braces {}.
Relations Between Sets
There are two basic relationships between sets: equal sets and subsets.
Equal Sets
If two sets have the same elements, we say the sets are equal, and write A = B if our sets are A and B. If they are not equal, we use the sign. For example A B.
Subsets
Another relationship between sets that is very important is the concept of a subset. We say A is a subset of B if all the elements of set A are found in set B. Symbolically, A is a subset of B would be written like this,
There are two notations for subset, if A is a proper subset of B, we would show it symbolically like this,
It would mean that all the elements of A are in B, but set B has at least one other element not in A.
Example 1
If A = {1, 2, 3} and B= {1, 2, 3, 4, 5} we would say A is a proper subset of B, or A⊂ B since all the elements of A are in B, but B has the elements 4 and 5 that are not in A. Sometimes it helps to remember that set B must be larger since it has at least one element more than A.
On the other hand, if A = {a, b, c} and B = {All lowercase letters from a to c} then but not a proper subset.
As the example above demonstrates, a set is a subset of itself, but it is not a proper subset. If A is a subset of B and it is possible that A=B then we use the notation
Note the line under the subset notation helps you remember that these two sets could be equal.
Example 2
Is { } a proper or improper subset of the set B = {1, 2, 3}?
Yes, it is a proper subset because all of { } is in set B, and B contains at least one other element not in { }. It might help to consider this: if you take out the 1, 2, and 3, what is left? The empty set, of course! This leads to the following rule.
The number of subsets of a set is completely determined by the number of elements in the set. It has nothing to do with what the elements are. If a set A has n elements then it must have subsets. For example if A is a 3 element set, say A={1,2,3}, then there must be subsets of A. Let's list them to make sure. They are {}, {1}, {2}, {3}, {1,2}, {1,3}, {2,3}, {1,2,3}. Similarly, if B is a set with 5 elements, there will be subsets of B.
Operations on Sets and Venn Diagrams
The universal set U is the set containing all the elements you are currently considering.
Example 1
If you were working with sets of colors, the universal set would be the set containing all possible colors. If you were working with sets of planets, the universal set would be the set containing all the planets.
Does it seem logical to say that for any set A in the universal set, A ⊆ U? The answer is YES!
Venn Diagrams
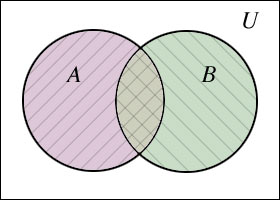
We need some way to discuss sets without listing all the elements in order to show certain relationships between the sets. Venn diagrams have one or more circle/s that represent set/s inside a rectangle, where the rectangle represents the universal set.
Figure 1 shows a universal set containing two sets: A, and B. The overlapping of sets A and B indicates the possibility that some elements are common to both of these sets. These common elements would be found in the overlap area.
Two Basic Operations on Sets
In arithmetic, we have the binary operations of addition, subtraction, multiplication, and division; in set theory we also have operations. Two basic operations are called union of sets and intersection of sets.
Operation 1: Union of Sets
The union of two sets A and B results in another set that includes all of the elements in A together with all of the elements in B. In other words all of the elements that are in A or in B. The symbol we use for union of sets is ∪.
Example 1
Suppose that A = {1, 2, 3} and B = {1, 3, 5, 7} then A∪B would be the set {1, 2, 3, 5, 7}.
Does it make sense to say that A∪{ } = A? If you take all of A and add nothing, what do you get? The set A, of course.
Operation 2: Intersection of Sets
The second basic operation on two sets is intersection. By the intersection of sets A and B we mean the set having those elements that are common to both A and B. The symbol we use for intersection is ∩.
Example 2
If we have a set A = {1, 3, 5, 7} and B = {3, 4, 5}, then A∩B would be the set {3, 5}. Note, these are the only elements common to both sets.
Finding the intersection of sets is like sorting socks after doing a wash. You have two piles of socks from the wash and you put the matching socks together and set them in the laundry basket to distribute to the family. The paired socks in the laundry basket represent the intersection of the original two piles of socks.
Earlier, we talked about the union of a set A and the empty set resulting in set A. Can you see what the result would be if we intersect a set A with the empty set? If you think for a minute, it should be obvious: the intersection must be the empty set, since you cannot have anything in common with a set containing no elements.
Disjoint Sets and Complementary Sets
Before we move on to two more operations, let's learn what "disjoint sets" are.
Disjoint Sets
Two sets A and B are called disjoint if they have no elements in common.
In this case the intersection will be the empty set. Now look again at Figure 1 in section 7.1. Are sets A and B disjoint? This is more difficult to answer because they are showing an area of intersection for the two sets in the Venn diagram. Since this particular Venn diagram is only showing the possibility that sets A and B could have some elements in common, we cannot say for sure whether A and B are disjoint or not.
Example 1
If we knew that set A contained the elements {1, 2, 3} and set B contained the elements {5, 6, 7}, then the intersection of sets A and B would be { }, which is the empty set. So, in this case sets A and B are disjoint.
Operation 3: Complement of a Set
The complement of a set A, written , is the set of all those elements in the universal set, U, that are not in A.
Example 2
If the universal set is the set {1, 2, 3, …, 10} and , then .
If you think about it, it is apparent that any set and its complement will always be disjoint.
What is the complement of the universal set? The empty set.
Properties of Sets
De Morgan's Properties
Two more properties dealing with set operations and complements are known as De Morgan's properties.
, and
How would you go about proving these properties are true? You could pick some set to be the universal set. Next, define A and B and their complements. Then show that the properties are true. But this would only show that the property holds for this specific example; we need to show that it works all the time.
To show it works for all sets we could use a Venn diagram that demonstrates all the possibilities when considering any two sets in a general universal set. Note the following Venn diagram and how its particular configuration covers all possible cases with two sets in a particular universal set.
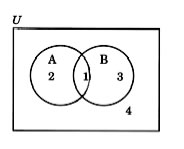
The numbers in the following Venn diagram will be used to denote certain areas in the upcoming discussion.
Area #1 denotes the intersection of sets A and B.
Areas #1 and #2 denote set A.
Areas #1 and #3 denote set B.
Area #4 denotes the area in the universal set not in A or B.
would be areas [#1, #2, and #3].
would be area [#1].
complement is areas [#3 and #4].
complement is areas [#2 and #4].
Now let's prove the first of De Morgan's properties: .
To determine the left side of the equation we realize that A∪B is area [#1, #2, and #3], so the complement of those areas would be area #4. Therefore the left side gives area #4.
To determine the right side of the equation understand that A is area [#1 and #2], so the complement of A is area [#3 and #4].
B is area [#1 and #3], so the complement of B is area [#2 and #4].
The intersection of A complement and B complement is area #4. Therefore, left and right sides of the equation match and the first property is proven.
Can you prove De Morgan's second property? Why don't you try it and when you think that you have it figured out, click to see the Instructor's Solution.
To determine what areas the left side of the equation results in, realize that is just area #1, therefore the complement of is areas #2, #3 and #4. Thus the left side gives us these three areas.
On the right side we start with the complement of A which gives areas #3 and #4 (since A is areas #1 and #2). And likewise, the complement of B is areas #2 and #4. When we take the union of those two complements we include all of the areas #2, #3 and #4. Therefore we see that the right side of the equation gives the same areas as the left side and they must be equal.
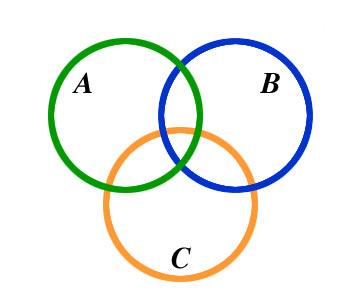
Note the Venn diagram, below. In this Venn diagram we have three sets in our universal set and a total of eight areas we could use as areas to reference. Every time that a new set is added the number of different areas doubles.
Counting Elements
Number of Elements in a Set
To denote the number of elements in a set, we use the notation n(A). This is called cardinality of a set A. Putting the lowercase n in front of the set in parentheses refers to the number of elements in the set. For example: If A = (2, 4, 7, 9) we would say n(A) = 4. If we can assign a positive integer or a zero value to n(A), then set A is finite; if we cannot, then set A is infinite.
Carefully go over Example 2 in Section 7.2 in the text to see how the formula for the number of elements in the union of two sets is derived.
If the sets are disjoint then the last part of the formula would be zero. Many students make mistakes by forgetting this last part of the formula and end up adding the elements in the intersection twice.
Let's look at some examples and try to pull the various ideas presented above into clearer focus.
Example 1. Sets with Numbers
Let A = {3, 4, 7, 8, 9} and B = {4, 7, 12, 15} in the universal set
{1, 2, 3, …, 15}.
If we want to find , we would first have to determine . So would then be 7.
To find using the formula we would have to find the intersection . Then is 2.
Could we use the above formula for to get the same answer? Let's try it.
What about A complement? Did you get ? Remember ={1, 2, 5, 6, 10, 11, 12, 13, 14, 15}. So the answer should be =10.
Example 2. Sets with Letters
What about sets with letters instead of numbers? Are they done differently?
, then what is ? Since , then .
Example 3. Sets with Mixed Elements.
If the universal set is {0, 1, 2, …10} and A = {0, 2, 4, 6, 8, 10} and B = {prime numbers less than 10}, find the following:
(Hint: You didn't forget what the prime numbers were, did you?)
Example Problems (Selected from Section 7.1)
In this lesson, the way to solve selected problems from the Sullivan text in section 7.1 and 7.2 will be demonstrated. The problems selected from Exercise 7.1 include #16, #28, #33, and #52 on page 364 of the text. Click on the thumbnail or the problem title bar below the video to select, and watch how an instructor solves the problem.
Section 7.1
Exercise 7.1: Problem 16 Transcript
Hello. We're going to do an example problem here. This is from section 7.1. This is problem number 16 from the homework. This is a true/false question. We're going to look at a set statement and determine whether it's true or false.
The way to do these problems is to work with the sets, determine two final sets, and, in this case, we're going to determine whether one is a subset of the other.
So the question says, one, two, three, union, three, four, five, and is a subset of three, four, five. So we're going to determine whether this union is actually going to end up being a subset of three, four, five.
The way to do the problem is to perform the union, come up with the final result there-- of course the union takes the two sets and puts them together and makes one bigger set-- and then look at the final result and see if it's a subset of three, four, five.
So the union of one, two, three, and three, four, five, is one, two, three, four, five. And the question is, is that a subset of three, four, five?
Now, a subset would mean that all the elements in this set are also elements in that set, and that obviously, is not true. So this is a false statement. And that would be your answer.
The way to do the problems, when you're asked whether things are true or false, is to work them out, determine from your final results whether that's true or false. All right.
Exercise 7.1: Problem 28 Transcript
We're going to do problem number 28 from the homework from 7.1. I'm going to show you how to work through this problem. There's a variety of different things we're going to be doing. There's six different parts to this problem. This is a pretty good example of one that does a whole bunch of different things.
The sets that we're working with, the universal set is going to be a, b, c, d, e, f. The set A is going to be b, c, and the set B is going to be c, d, e.
Part a. We're going to take A union B. So we take the sets A and B, and we put them together to make one big set. That's going to be b, c, d, e. That takes all of the elements from both of the sets and make them one big set.
Part b. A intersect B. The intersection of two sets is the overlap. It's the elements that are both in A and in B. And that, of course, is just the element c.
Part c A bar. Those are all the elements that are in the universal set, but not in A. So if you look at the universal set, start going through it, and just include the ones that are not in A. So a, small a of course, lower case is not in A. b and c are in A, but d is not. e, f, and that's A bar.
Part d. B bar. All of the elements that are in the universal set, but not in B. That would be a, b, and f. So those are all of the things in B bar.
Part e. A intersect B. Bar over the whole thing. You have to pay particular attention because order of operations becomes important on a problem like this. And this problem, you want to do A intersect B first. And then complement that. It's not a matter of taking A complement and B complement, and then intersection. So order of operations is really important with these. So we're going to find A intersect B. I'll do that down here, I guess. A intersect B, we already figured out was c. I guess I didn't have to do that. And then A intersect B complement was a, b, not c, d, e, and f. So pay particular attention to those, and which order things are done in.
Part f. On the other hand, A union B complement. Once again, when the bar's over the whole thing as opposed to barring each A and B separately then unioning that, you find A union B first. And then complement. So, we already know that A union B is b, c, d, e. So A union B complement is a, b, of course is a, f. That's all the elements that are in the universal set, but not in A or A union B. OK.
Exercise 7.1: Problem 33 Transcript
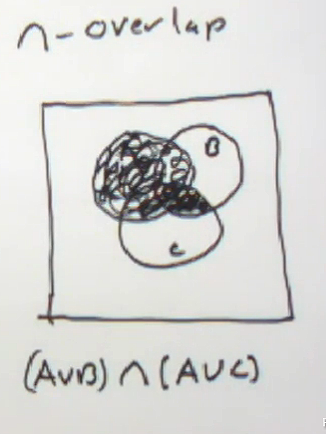
This time we're going to do another problem from 7.1, question number 33. This is a Venn diagram question. There's a bunch of Venn diagram questions from this section. Some are two set, some are three set. This is a three set problem.
We're being asked to illustrate the Venn diagram for A union B, intersect, A union C.
It's a three set Venn diagram because you have the set A, B, and the set C. We're going to do this in two pieces. When they become complicated enough, a lot of times it's good to do the set up on one Venn diagram, and then the final result on another one.
Over here, to the left, we're going to do our set up Venn diagram. We'll have three circles, A, B, C. And we'll illustrate the two parts, A union B, and A union C. We'll do those in different colors so that you can see the different contrast. For A union B, we'll do forward slashes in yellow. So A union B, will be these. And then for A union C, we'll do backslashes in orange.
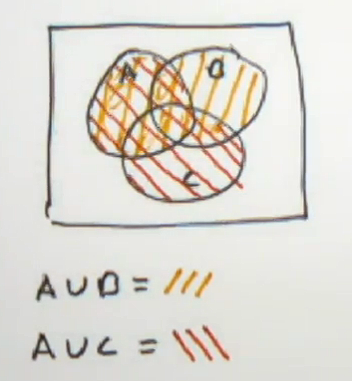
So A union C is everything inside the A circle together with everything inside the C circle. Of course it's this up here also. And this a little bit down here. Now, the intersection of those two sets is the overlap.
If I were doing to union here I would include everything that's shaded in, but since this is an intersection it's just going to be where those two sets overlap. And if we just outline this right here, we can see they're overlapping in here, and they're overlapping in here, and they're overlapping in the A circle. So our final result is going to be this. The A circle with this little knob sticking off to the side. So maybe we'll just do that. We probably don't need to at this point, but just to make things a little bit clearer.
A union B, intersect, A union C, it's going to be, there's your A circle, there's your B circle, there's your C circle. And the final result will be everything on the inside of the A circle, and this is a little bit right here. So that is your answer. OK.
Exercise 7.1: Problem 52 Transcript
We're going to look at question number 52 from section 7.1. This is a translation question. We have a bunch of sets. The universal set is all college students. The set M is male college students. Set S is smokers—smoking college students. College students who smoke would be better, but we'll just go with that. And F is freshmen&mdsah;college freshmen, of course.
U=all college students
M=male college students
S=smoking college students
F=freshman
And we're supposed to take the statement F union S union M and translate that using these statements. So you have to be a little bit careful here. There's a temptation to want to say freshmen or smokers or males.
But that's a little ambiguous. We want to be clear about what's going on. We want to make sure that we're being clear that we want to include college students that have not just all those properties together, but any college student that has any of those properties or any combination of those properties. OK?
So we're going to go with the set of all students who are freshmen or male or smokers or any combination of these. So it could be freshmen smokers, male smokers, freshman male smokers, or any combination of those. OK.
Example Problems (Selected from Section 7.2)
In this lesson, the way to solve selected problems from the Sullivan text in section 7.1 and 7.2 will be demonstrated. The problems selected from Exercise 7.2 include #14, #32, and #38 on page 369~371 of the text. Click on the thumbnail or the problem title bar below the video to select, and watch how an instructor solves the problem.
Section 7.2
Exercise 7.2: Problem 14 Transcript
We're going to look at problem number 14 in section 7.2 here. We're working with the number of elements in a set. We're going to do this one a couple of different ways using a Venn diagram, and also using the formulas. So, number 14.
The information that we're given is that the number of elements in A is 10. The number of elements in A intersect B is 5. And the number of elements in A union B is 29. And we're supposed to find the number of elements in B.
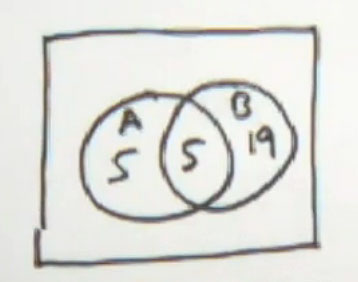
So let's do that using a Venn diagram first. And then we'll go through it using the formulas. I lean towards Venn diagrams a little bit. Students generally have more success once they learn how to do these. But in a lot of cases, the formulas work perfectly well, also. So there's your two set Venn diagram. We only have two sets here.
You always need to fill in the area that is given to you with two pieces of information. You can't put the number 10 anywhere on here, because the number of elements in A is 10. That includes this area and this area. Some of the 10 are going to be in here, and some are going to be in here.
However, we do know that the number of elements in A intersect B is 5, so we do this. Now of course, if the total inside the a circle has to be 10, and this is 5, then this is going to be 10 minus 5, and this one is also going to be 5. Now we have 10 inside the a circle, 5 inside A intersect B.
Now, we also this piece of information that the number of elements in A union B is 29. So the total inside the two circles has to be 29. There's 10 here. That means 29 minus 10 is 19 have to be inside that B circle. So how many are inside B? Well, not 19. But inside that B circle, the total inside the B circle is 24. Sorry. 19 plus 5.
Now, we can also do that using a formula. Remember the formula n of A union B is equal to n of A plus n of B minus n of A intersect B.
The formulas work perfectly well in a lot of cases, not in all cases. We know this is 29. We know that this is 10. We know that we're looking for this one. And we know that this is 5.
So this is 29 equals 5 plus n of B. And bring the 5 over, solving this algebraically. And then n of B is equal to 24. So you could do it that way, also. In this case it's probably a little easier to use the formula, but there's a lot of cases where the Venn diagram is the way to go. So there's two different ways to do the same problem. OK.
Exercise 7.2: Problem 32 Transcript
We're going to look at question 32 from section 7.2. This is a table. I'm not going to recopy the table for you, that's in your textbook. It's a table, a contingency table that looks at the industry type for CEOs as well as the region that they're in. Industry types are manufacturing, communications, or finance. And then the regions are Northeast, Southeast, and Midwest. And all we're going to do is do some totals here.
Part a, the question is, What is the number of CEOs whose response was not Southeast? So not Southeast, of course, is Northeast, or Midwest, or West. Or means add.
There are 102 in the Northeast. That's 37 + 35 + 30. In the Midwest there are 52. 27 + 15 + 10, which is 52. In the West, there are 53. 15 + 20 is 35 + 18 is 53. And that gives us a total of 207.
NE=102
MW=52
W=53
102+52+53=207
Part b. So on the other hand, in part b they ask us for the number of CEOs whose responsible was communications or West. Now there in the West, we already decided there were 53. In the communications, 35 + 23 + 15 + 20 is 93. So, communications. There are 93. In the West there are 53.
And communications or West, you might think of them as just being 93 + 53. But you have to be a little bit careful here. Seems like you might have double counted something. Those people that are in communications and in the West are actually counted in the West column, and they're also counted in the communications row. You don't want to double count that.
So we should subtract that 20 off once, and that will bring it back to the count that we want. So comm or West is going to be 93 + 53 - 20 and that is 126. Add them together, subtract off the one that you counted twice, and now you're only counting it once.
Comm=93
West=53
Comm or West= 93+53-20=126
In Part c, we want the number of CEOs whose response was Northeast, but not manufacturing. So Northeast, but not manufacturing is just our 35 plus our 30 for communications and finance. And that is a total of 65.
35+30=65
Part d. On the other hand, in part d, the number of CEOs whose response was manufacturing or communications or Midwest or West, let's see, that's manufacturing the first two rows. Total those up. Or Midwest. And West. So the last two columns, we could total those up. Add those all together, make sure we didn't double count too much stuff. Subtract it off if we did, but there's actually going to be an easier way to do this. That seems complicated.
If we take manufacturing communications, West and Midwest, that fills out the entire top right part of that table, and only leaves the finance Northeast, and finance Southeast blank. So instead of counting everything that we want to include in, we just throw away the things we don't want using the complement. That's going to be an easier way to do that.
So we know there are a total of 250 CEOs, and we're going to subtract off the 30 and the 12 that came from Northeast and Southeast in finance.
That's 250 - 42, which is 208. So that's a far easier way to do that than adding all those other numbers.
250-(30+12)=208
OK.
Exercise 7.2: Problem 38 Transcript
We're going to look at problem number 38 from section 7.2. This is a problem that's most easily done using a Venn diagram. This is a three-set problem. It's a survey of 75 business travelers, and it's a survey of what they normally read - which newspaper. So I'm not to read off all the numbers to you, I'll leave that to you.
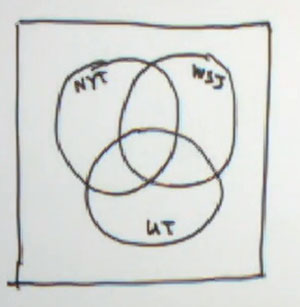
But we have The New York Times, The Wall Street Journal, and USA Today that we're going to be working with as our newspapers. You need to fill these in very carefully. This will be The New York Times. This will be The Wall Street Journal. And this will be USA Today. So they give us numbers. How many read The New York Times, how many read the Wall Street Journal, etc., and then they give us combinations.
New York Times and Wall Street Journal, New York Times and USA Today. And they give us all three. We just have to start in the middle, with all three. So they tell us that there are 5 that read all three. And then we have to work out slowly. This has to be done just right. They tell us that 8 read The Wall Street Journal and USA Today.
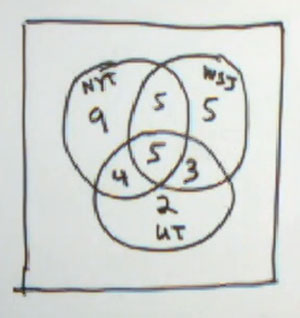
So you know that in here, between The Wall Street Journal and USA Today is going to be 8. Now, 5 of them are here, so you need to make sure you subtract at this point to get the 3 there. That's a total of 8 that read The Wall Street Journal and USA Today. On the other hand, they tell us that nine read the New York Times and USA Today.
Five are here. At least 4 for right there. Make sure you're subtracting as you're filling these in. 10 read The New York Times and The Wall Street Journal. 5 here, 5 here. We're going to have to subtract again in this next set of steps. They tell us that 14 read USA Today. There's a total of 12 right here that are inside the USA Today circle.
So we only need two more to get the total up to 14 that read USA Today. On the other hand, they tell us that 18 read The Wall Street Journal. There's 13 already inside The Wall Street Journal circle. So we need 5 more to make that total 18. 23 read The New York Times. There are 14 right there.
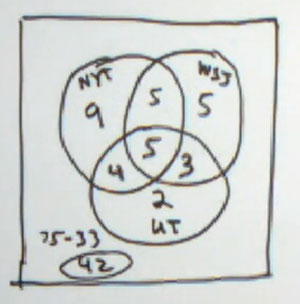
That leaves 9 for inside The New York Times circle, but outside the other circles. Now, there are a total of 75 business travelers. Let's see, there's 23 right here. There's 31 right there. There's 33 right there. And that means outside we have 75 minus 33, which is 42 that are inside any of those circles. OK.
So we've got our Venn diagram all filled in now, we're ready to start answering questions.
Part a. how many read none of these three magazines? That's the 42 we just found.
Part b. How many read The New York Times alone. That means The New York Times and neither of the other two. That's our nine. right there.
Part c. How many read The Wall Street Journal alone? That is our 5 right there. Wall Street Journal but none of the other - 2.
Part d. And USA Today only. And that is this 2 right here.
Part e. How many read neither The New York Times nor The Wall Street Journal. So they don't read The New York Times, and they don't read The Wall Street Journal.
So you can't include anything that's inside either of those two circles. And if you're not thinking very carefully, you might think that that's just 2. But we also have this 42 down here, and they certainly don't read The New York Times or Wall Street Journal. So we have 2 plus 42, which is 44.
And Part f. How many read The New York Times or Wall Street Journal, or both? So all of The New York Times people, all the Wall Street Journal people. And all those that are both, of course. Well, there were 23 inside The New York Times circle plus 5 plus 3 23 Plus 5 plus 3 is 31.
So that's how you want to do that, filling that Venn diagram in carefully. Making sure you subtract at each step, and then picking out the important areas, and sometimes it might be more than one. OK.
Lesson 1 Activities
Lesson 1 Practice Problems
Please complete these problems in the textbook so that you will be prepared for the graded assignments. The answers to these questions are in the back of the book, so you may check your work.
- Section 7.1: 1–57 odds.
- Section 7.2: 1–45 odds.
Lesson 1 Homework
Please complete these problems in the textbook with your Wacom Bamboo Pen and Tablet, or by hand and then scanned into a file. Submit your work to the dropbox.
- Section 7.1: 26, 30, 34, 46, 50
- Section 7.2: 12, 16, 22, 30, 36
Lesson 1 Practice Quiz
There are 10 questions in total. The grade will not be counted into the final grades.
There is no time limit for this practice quiz.
The Lesson 1 Quiz will open on the first day of the lesson.
Lesson 1 Quiz
For this quiz, there are 10 questions in total. The full grade is 100 points.
Caution: This is a timed quiz with only one attempt allowed. Once the quiz is delivered the clock starts and will not pause even if you leave the quiz. Be mindful of the time remaining, and please make sure that you submit the quiz before time runs out.
You are not allowed to right-click, print, etc. The system will automatically submit your quiz when time limit expires.