Main Content
Lesson 2: Distributions
Finding Values of
Because Z is a standard curve, often we’re asked to find some value of Z for a given probability. In other words, given an area α (i.e., probability) under the curve, what is the corresponding value of on the horizontal axis that gives us this area?
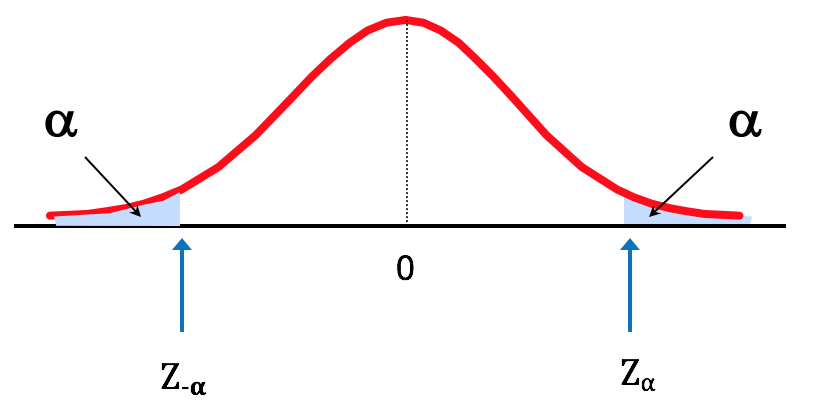
Figure 2.16. Finding the Z-score for a Given Probability
Let's consider how this is used in the examples we have seen before.
What Is the 95th Percentile Score for IQ?
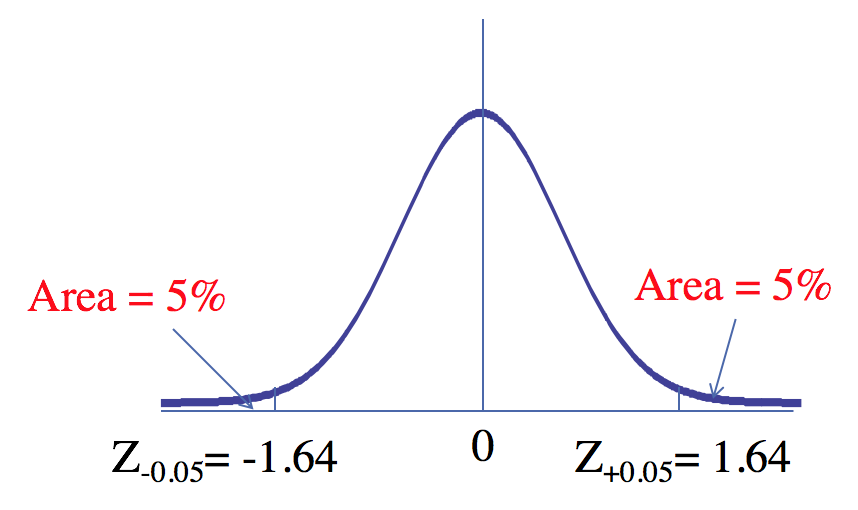
Sometimes, we are interested in knowing percentile scores (e.g., your GMAT scores). A 95-percentile score (or the top 5th percentile score) implies that out of 100, only 5 score above this score and 95 score below this score.
We write this as . What is the value of Z for which only 5% of all values are higher than Z?
In this case:
Figure 2.17. What Is the 95th Percentile IQ Score? (α = 0.05)
In Excel, we use the function NORM.S.INV (p); p is the white portion of the curve.
Note the "+" sign in . This signifies that we are talking about the top 5 percentile. will signify the bottom 5th percentile.
If IQ is distributed with a mean 100 and standard deviation 15, the 95th percentile (or top 5 percentile score) is
100 + 15*1.644854 = 124.6728
For example:
Why Learn All These Formulas?
As you will soon see in the next lessons, knowing the z-distribution helps immensely in statistical inferencing. We can always convert an observation (i.e., the value of a variable) into a z-score to tell us how many standard deviations above or below the mean that observation is. More importantly, we can also calculate how extreme the value of a variable needs to be to satisfy a certain probability.
