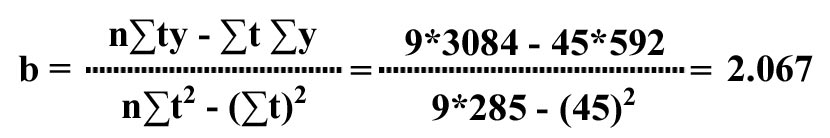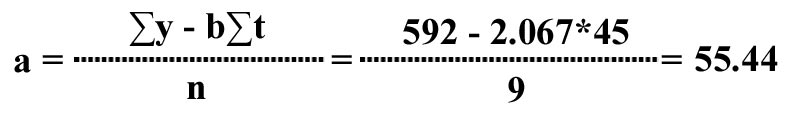Example of Linear Regression

The historical data on the cost (in hundreds of $) for a project activity is given below. Develop a trend equation using Linear Regression Analysis and forecast the cost of this activity for period 10 and 15.

t	y
1	58
2	57
3	61
4	64
5	67
6	71
7	71
8	72
9	71

The calculations for determining the slope and intercept of the regression line are shown below

t	y	t*y	t²	y²
1	58	58	1	3364
2	57	114	4	3249
3	61	183	9	3721
4	64	256	16	4096
5	67	335	25	4489
6	71	426	36	5041
7	71	497	49	5041
8	72	576	64	5184
9	71	639	81	5041
t = 45	y = 592	t*y = 3084	t² = 285	y² = 39226

The slope b of the line is given by:

The intercept a of the line is given by:

Hence the linear trend equation is given by:

y_t = a + bt = 55.44 + 2.067t, and

The forecast for period 10 is given by

y₁₀ = 55.44 + 2.067*10 = 55.44 + 20.67 = 76.11

For t = 15, y₁₅ = 55.44 + 2.0667 *15 = 86.445

In the discussion and example above on linear regression analysis, the independent variable was t--the time period. However, the linear regression technique can also be used determine association or causation between two variables. In such cases, we use the notation x for the independent variable and y for the dependent variable. The linear regression equation in such cases would be of the form

y_c= a + bx_i, where

The slope b of the regression line is given by:

.

The intercept a of the regression line is given by:

.