MANGT 515 Prospective Students
Sample Syllabus
Sample Lesson
Introduction
2.1 Reasons for Forecasting in Project Management
2.2 Forecasting Methods for Projects
2.2.1 Qualitative Forecasting Methods
2.2.2 Quantitative Forecasting Methods
Time Series Analysis
Short Term Forecasting Methods
Naïve Approach
Simple Averages
Moving Averages
Exponential Smoothing
Example of Exponential Smoothing
Trend-Adjusted Exponential Smoothing
Example of Trend-Adjusted Exponential Smoothing
2.3 Intermediate Term Forecasting
Example of Linear Regression
Evaluating the "Fit" of the Regression Line
2.3.2 The Correlation Coefficient (r)
2.3.3. The Standard Error of the Estimate (syx)
2.3.4 Limitations in Forecasting Using Linear Regression
2.3.4 Limitations in Forecasting Using Linear Regression (continued)
2.4 Forecasting the Project End Conditions
2.5 S-curve Forecasting
2.6 Technological Forecasting*

Evaluating the "Fit" of the Regression Line

The nest step in regression analysis after obtaining the regression line is to evaluate how well the model describes the relationship between variables, or how good is the line of "best fit". Three measures can be used to evaluate how well the computed regression line fits the data. These are: The Coefficient of Determination (R2 ), The Correlation Coefficient (r), and The Standard Error of the Estimate (syx)

The Coefficient of Determination (R2)

Three Measures of variation can be computed in linear regression analysis. These are:

  1. Total sum of squares (SST)
    This measures the variation of the actual Y-values around the mean Y.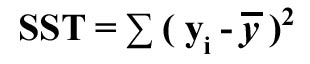

  2. Explained variation (SSR) or the regression sum of squares
    This measures the variation due to the relationship between X and Y, i.e., the difference between the mean Y and the predicted value Y using regression.

  3. Unexplained variation (SSE) or error sum of squares
    This measures variation not explained by regression, i.e., variation due to other factors or variables not included in the regression model.

  4. Coefficient of Determination (R2)
    This is the proportion of variation explained by regression (i.e., by the relationship between X and Y). The formula to compute R2 is: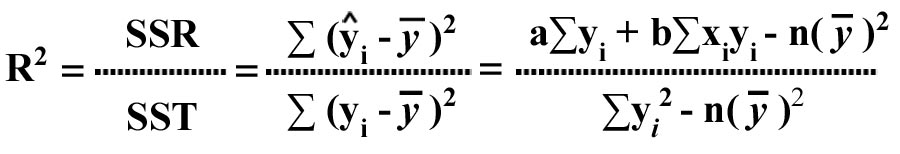

R2 takes on a value between 0 and 1. The higher the value of R2 the better is the line of fit.